Scale: Beyond the Earth’s paper-thin atmosphere

In yesterday’s blog entry, we tried to come to grips with the actual thickness of the Earth’s atmosphere. To do so, we drew the first four layers of the atmosphere to scale on a single piece of A3-sized paper oriented in the portrait direction. In this model, it was determined that, if the first four layers of the Earth’s atmosphere could indeed fit within a span of 42 cm, then the size of the Earth in this model would need a radius of 53.5 meters. To help put these dimensions into further perspective, imagine a normal-sized apple: the ‘flesh’ of the apple is the Earth, while the apple’s thin skin approximates the thickness of the Earth’s atmosphere!

We then asked four questions of our Earth/Atmosphere model. Each of these questions, and their answers, are presented below.

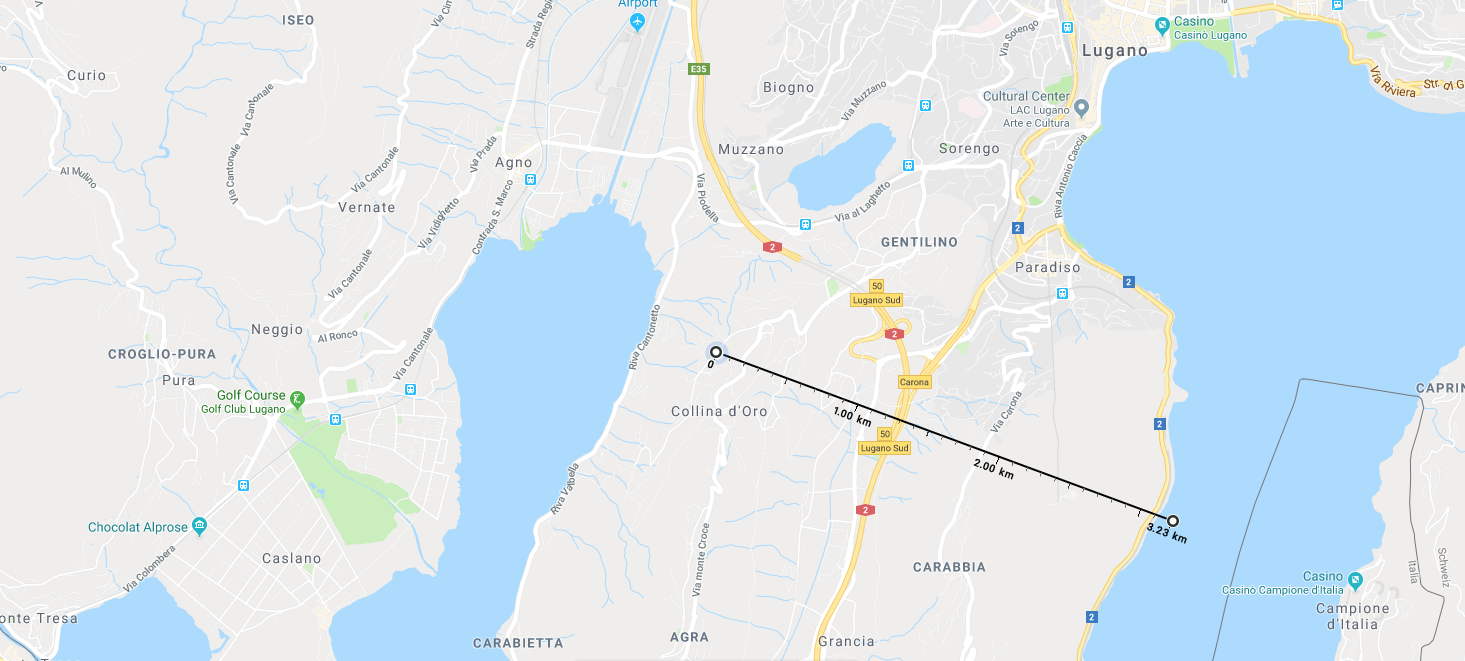
If our model Earth here on the TASIS campus has a radius of 53.5 m, how many kilometers (km) would we have to travel from campus in order to arrive on the surface of the Moon?

• Answer: 3.23 km from the TASIS campus, which would actually put us into Lago di Lugano if we were to walk 3.23 km from TASIS in a southeastern direction towards Campione d’Italia. [In terms of actual distance, the real Moon is somewhere around 384,400 km away from the real Earth.]

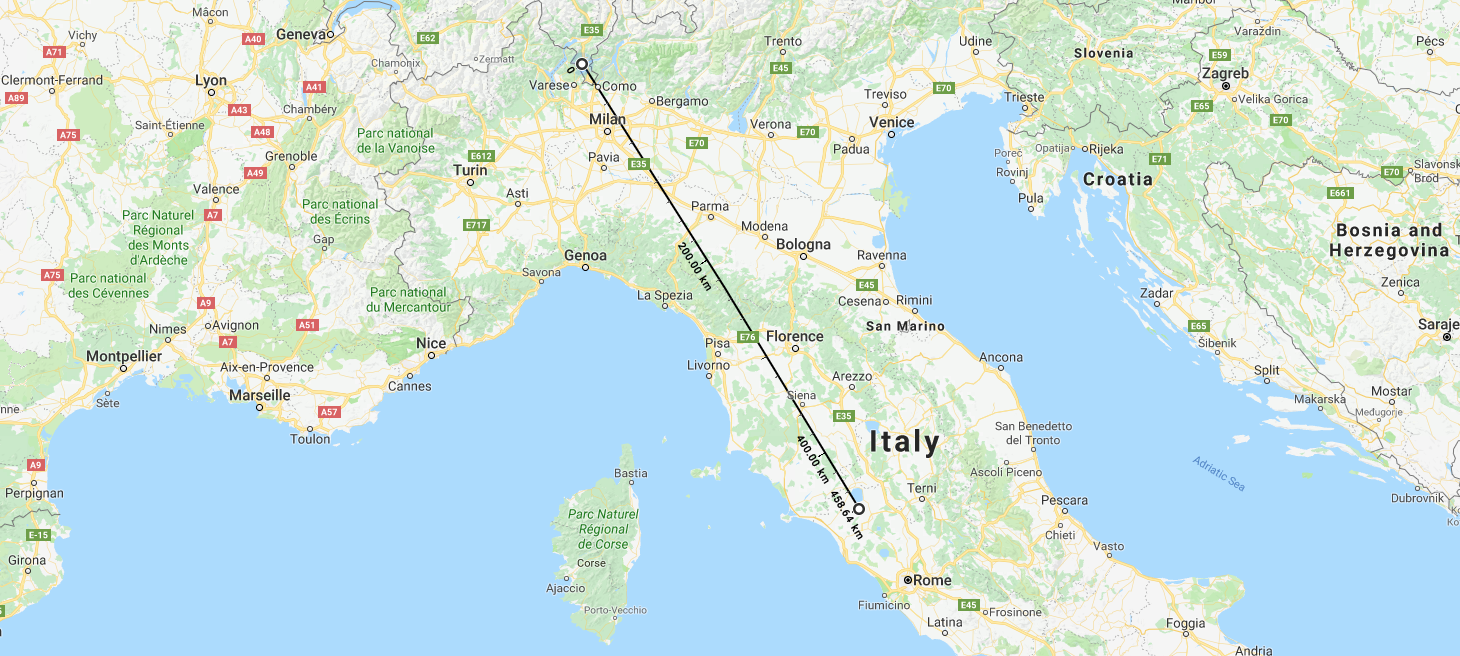
If our model Earth here on the TASIS campus has a radius of 53.5 m, how many kilometers (km) would we have to travel from campus in order to arrive on the surface of the Mars?

• Answer: 458.64 km from the TASIS campus, which would actually put us into central Italy if we were to walk458.64 km from TASIS in a southeastern direction towards Roma/Rome, Italy. [In terms of actual distance, the real Mars is somewhere around 54,600,000 km away from the real Earth.]

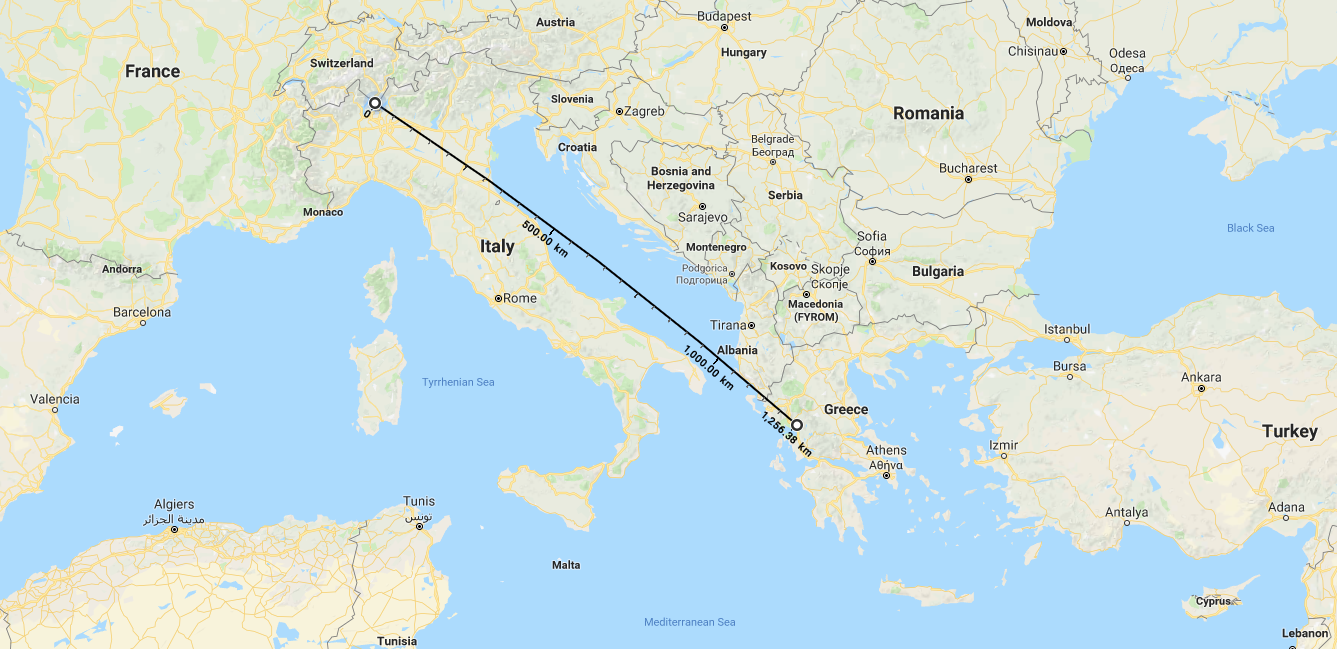
If our model Earth here on the TASIS campus has a radius of 53.5 m, how many kilometers (km) would we have to travel from campus in order to arrive on the surface of the Sun?

• Answer: 1’256.64 km from the TASIS campus, which would actually put us into Lago di Lugano if we were to walk1’256.64 km from TASIS in a southeastern direction towards Athens, Greece. [In terms of actual distance, the real Sun is somewhere around 149,600,000 km away from the real Earth.]

If our model Earth here on the TASIS campus has a radius of 53.5 m, how many kilometers (km) would we have to travel from campus in order to arrive on the surface of Alpha Centauri–the nearest star which is not our Sun?

• Answer: 336,000,000 km from the TASIS campus, which would actually put us…well, that’s a bit more difficult to say. Since the Earth is about 40,000 km in circumference at its thickest point, the equator, one would need to make about 8’400 complete laps around the Earth’s equator in order to travel 336,000,000 km!!! So, we can’t really put a ‘dot’ on the Earth to represent the distance needed by the conditions or our model. [In terms of actual distance, the real Alpha Centauri is somewhere around 40 trillion km (40,000,000,000,000) away from the real Earth.]